Cold Fusion? Again?

Sorry, another break from our study of quantum mechanics. I couldn't resist when I came across a very interesting story. A h/t to Weird Things for posting this about a month ago. Greg Fish's post discusses a pair of Italian experimental physicists that claim to have developed a reactor capable of creating power with very little energy input. Since a month ago, news has spread about this experiement, but is it real or are we looking at a repeat of the claims started Pons and Fleischmann's famous cold fusion experiment? This remains to be seen, but the idea is certainly interesting.

I would like to direct you to this article from Popular Science. The claim is that Andrea Rossi and Sergio Focardi have successfully constructed a reactor capable of 12,400 kW from a 400 W input on a tabletop device. Instead of using palladium electrodes like Pons and Fleischmann's apparatus, this device supposedly fuses nickel with hydrogen and produces copper and energy.

A translated interview with Andrea Rossi sheds a little light on the device, but they are keeping details quiet until they have a better understanding on the theory behind it. There still isn't much information about this out there, but I'm keeping my eyes open and will post an update as soon as I can. This is certainly intriguing. If anything positive comes out of this, it will certainly be exciting, but I for one remain extremely skeptical, and will remain skeptical until either we see these in action or the theory behind it is explained.

It'll blow your mind - part 2

Well I read the full paper and I must say, it's a difficult topic. Those who have personally asked me how you can actually measure something being in two states at the same time will hopefully find an answer here.

Quantum mechanics has been well established by experiment. The theory behind this systems involved in this experiment are well understood. That being said, it is a comparison between the gathered data and what they theory predicts that leads the physicists who performed the experiment to conclude that they are observing a macroscopic quantum effect (the drum both vibrating and not at the same time.). Let me try to explain.

The experimental set up is a extremely cold piezoelectric oscillator electrically coupled to a quantum bit (or, qubit). If none of those words make sense, let me break it down for you. A piezoelectric material is a material that produces electricity from being bent or vibrated. You have seen piezoelectric materials in many places, perhaps the most familiar being in a butane lighter. When you click the lighter on, you are actually compressing a piezoelectric element that makes a little spark. The next word I would like to explain is the oscillator. An oscillator is something that vibrates in a predictable manor. Think of the surface of a drum. When you strike a drum, the surface moves up and down at a predictable rate - a drum is an oscillator. In this experiment, the piezoelectric oscillator is just a little piece of metal that produces an electric current when it vibrates. The physicists know at what rate (frequency) it can vibrate.

Next up is the qubit. A quantum bit is essentially a 1 or a 0 that obeys the laws of quantum mechanics. That is, a qubit is in two states simultaneously until measured. I do not pretend to be an expert in quantum computers, for some more information, I recommend Michael Nielsen's quantum computing for everyone. The basic idea behind this experiment is that when the oscillator vibrates, it affects the qubit. This allows the two systems to be entangled. Knowing the state of one means you know the state of the other. This way, the oscillator can be isolated (so that nothing is allowed to interact with it), and it's state can be inferred by qubit measurements.  Pretty cool.

Now, the most important part of the experiment is the cooling. The colder something is, the less it's molecules that make it up move, the less they move, the lower the energy. They cooled the oscillator down to EXTREMELY low temperatures so that it would have the lowest possible energy it can have (called it's ground state.). This corresponds it the lowest possible rate at which it can vibrate. They made measurements of the ground state vibration rate and the next to the lower vibration rate. The qubit's state was either 0 for the ground state or 1 for the first excited state.

Here's the part that's difficult to swallow. We can't actually look at the oscillator while we run this experiment because this would count as a measurement. Remember, measurements collapse the wave function to a single outcome. This is boring and there's no way we can observe quantum behaviour if we are constantly observing something. So how did they know they observed a large object obeying quantum mechanics? Well, they repeated certain measurements on the qubit. By repeating the measurements, they were able to measure the probability and the state transition times for the qubit. By comparing these probabilities and transition times to both the theoretical and experimental predictions of the qubit's behavior, they determined that they qubit was in a quantum superposition state (both 1 and 0 at the same time.). But, the qubit and the oscillator are linked, so knowing the state of one tells you the state of the other! Thus, they report with high confidence that the oscillator, which would be actually visible with the naked eye (but still very tiny) was in a quantum superposition state (being both in the ground state and first excited state at the same time!).

This is a major discovery! Provided others can replicate similar results in different experiments, this will confirm that everything, not just small objects obey the laws of quantum mechanics. Even trillions of atoms cannot escape the strangeness of the quantum world.

Comments? Questions? Mistake in my post? Open discussion encouraged!

Up next, the quantum mechanical spring, then a discussion and some demonstrations of expectation values!

Site News

Just a quick post here. It has been brought to my attention by my readers that my poll wasn't working. I believe I have fixed this. I'd love to get some feedback from you guys, so vote away! You won't hurt my feelings if my posts are "booooring," but you you select that option (or any other for that matter), I'd like some input on how to improve. Thanks!

Another matter my readers have mentioned to me is that my previous post was rather confusing. This is a difficult subject, but I'm going to go through the journal article once more to seek a better explanation. Stay tuned!

Old news, but it'll blow your mind...

... or at least it should. It blew mine back when I read it. Here is an article from Nature documenting a research effort in quantum mechanics. The research that this article discusses shows that even large objects can exhibit the weird quantum effects I've been talking about. I recommend reading the article, even though I'm not entirely pleased with some of the terminology (quantum mechanics is a tricky subject, and requires precise words to describe it.). If you're feeling lazy at the moment, my summary is below.

Andrew Cleland and his team of researchers at UCSB successfully measured an object large enough to be see with the "naked eye" exhibiting one of the most strange and difficult to swallow aspects of quantum mechanics. A quantum object can be in a state where it's moving, and a state where it's not - at the SAME time! These scientists were able to measure this in a tiny paddle that is 30 micrometers (that's about one thousandth of an inch!) in length. Here's a picture below:

This object is huge, at least in quantum terms. It's built out of trillions of atoms! What they observed is the object being simultaneously in a vibrating and stationary state at the same time! They did this by cooling the drum to 2 tenths of a degree Fahrenheit above the lowest possible temperature (absolute zero). This brought the molecules in the drum to their very lowest energy state. They were able to verify that it was not vibrating at all. With a quantum mechanical circuit, they could also bump up the energy level to make the drum vibrate at a VERY specific energy level. They put their circuit into what's called a quantum superposition state (a quantum state that is actually a mixture of two states, e.g. moving and not moving). The circuit was a superposition of telling the drum to be stationary, and to vibrate. What was the result? Exactly that! They were able to measure the drum as vibrating and not vibrating at the same time!

Let's review for a second. Why do we generally see small things follow the laws of quantum mechanics, but big things behave normally? This is because if something is really small, it doesn't interact with other things nearly as much. Think about someone you know (maybe yourself!) that had an extremely messy room. You couldn't walk around in their room without running into junk that was scattered about. Now think of the cleanest person you know. Perhaps you could walk across the entire room without running into anything! Back to the story, you are like the person in the messy room, and an atom is like a person in the clean room. An atom can move around a lot without hitting anything, but you cannot. Everywhere you walk, you run into air (air is made of trillions of molecules!). If you zoom in to an atom in the air, it's relatively far from the others. When you heat things up, the atoms move around a lot more, causing them to interact with other atoms. When you cool things down, they do the opposite, they hardly move at all, and hardly ever interact with the atoms around them. This is what they did, the slowed down all the molecules in the drum until they were barely moving.

This is really really cool and weird at the same time, you may ask what applications there are for this. The truth is, there aren't any right now, there's still working on that part. For those of you technically inclined, and with access to Nature, you can find a *.pdf of the article here. Anyone else think this is really really cool, or is it just me?

More on the "Particle in a Box"

The infinite square well problem previously discussed as typically called the "particle in a box" problem. This doesn't really make much sense in terms of the previous problem as it's more like a "particle on a line". Well, this problem is called the particle in a box problem because that's exactly what it describes and is used for. In this post, I will talk about one of the applications of this simple model. But first a video. Remember in the last post how I had the particle sitting there, it's it's probability distribution kinda melted? Well, here's the same thing, but now the particle is confined to a flat sheet instead of a wire.

Now, I find that really cool. You can really see the wavelike nature of the particle bouncing off the walls and running back into itself! It kinda looks like ripple on a pond, but water waves are made out of trillions of parts, but this is just one! What happens if I give it some initial momentum? Take a look.

The wave function also looks like this. Here's a couple more videos, one moving fast, and one moving slowly.

Here's the slow mover.

So what are these good for? Why do we care how a particle trapped in a box behaves besides the fact that it looks cool?

Well here's the biggest application I know of. Have you ever studied the ideal gas law? If you haven't, don't worry. It's a rather simple relationship between pressure, temperature, and volume.

PV = NkT

If you've seen it in the past, that's probably written a bit different than you're used to. This is how physicists express it, and since I'm a physicist... Anyway, P stands for pressure, V for volume, N for number of particles, k is called Boltzmann's constant, and T is absolute temperature. This equation says if you put a gas, like air, into a container you can calculate the pressure if you know how much air is in there, the temperature, and the volume. Also if you know the other three variables, you can figure out the last one. This equation is used a lot in many engineering and science fields.

Since I bring this up, was this equation originally derived from quantum mechanics? The answer is no. It wasn't. So why do I bring this up? Read on. This equation can be derived by experimental measurements on gases that are nearly "ideal".  An ideal gas is essentially a gas that doesn't affect itself, even when it is smashed down to a small area. Gases like Helium, or other noble gases, are very well approximated by the ideal gas law in certain cases. Using a gas such as this, a experimental physicist or chemist can derive this law. This law can also be derived using classical physics methods called "statistical mechanics", which uses probability and statistics to determine the properties of large collections of stuff. The reason I bring this up though is that you need quantum mechanics to get a full thermodynamic description of an ideal gas. That is, you need quantum mechanics to accurately derive its entropy. Entropy is a measure of the disorder of a system. Once you have the entropy, you can calculate other thermodynamic properties. I think the most remarkable thing you can do is re-derive the ideal gas law! Once you have the entropy, it's relatively easy to get the ideal gas law out of it. And where does all of this come from? That's correct, the particle in a box problem. Next time you think you don't deal with quantum mechanics always, think again, it's everywhere!

That's it for the infinite square well for a while, I may revisit it in the future, as it's such an important problem. Next up, I'm going to talk about something a bit more current and down to earth, stay tuned!

The Infinite Square Well

We've gotten past some of the fundamentals of quantum mechanics. Now it's time to begin one of the first problems encountered by physics students when studying quantum mechanics. It's the first not just because it's the simplest, but because it's important. It gives a solid example, and a way of thinking about many quantum mechanics problems.

So what is it? Well, the infinite square well is a particular choice of the Hamiltonian, or, the system. We have the usual kinetic energy term, but we have a particular potential. Imagine there's a particle. It could be an electron, a proton, a hydrogen atom. Anything small will do. We put this electron inside a very thin wire, so thin that it can only move forward or backward, not left or right or up or down. The electron can move perfectly freely inside the wire, but when it comes to one of the ends, it cannot help but bounce back. Think about you running in along a track. You keep running until you hit a wall. Since you're bored and got nothing else to do, you run the other way, until you hit the wall on the other side. You keep repeating this until you have enough bruises...

 

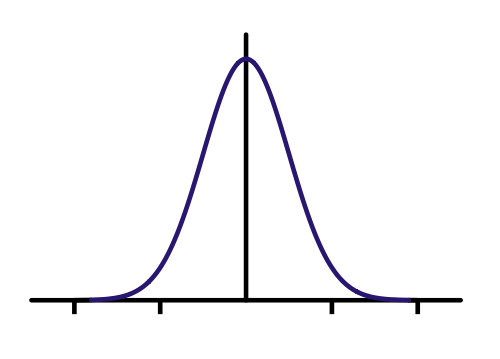
This is what the infinite square well represents. It's just an electron that's trapped along a line. We call it the infinite square well, because the wall is a barrier with infinte potential. That means you have to have infinite kinetic energy to go through! That's a pretty solid wall. It turns out, this is a decent model for electrons in a piece of metal. Here's where I think it gets cool. We solve Schrodinger's equation (SE from now on) and we get | psi >. At least, we get a way of determining how an initial state evolves with time. Let's say we put the electron in a wire and have a decent idea of where it is. It's probability density should look like a bell curve (known as the gaussian or normal distribution in probability theory.). Basically that says it's most likely at the center of the bell curve.

Here's a Gaussian curve. I made my initial state a bit skinnier because I think I know where I put the electron better. Let's see what SE predicts will happen to the probability density (just think of this as a guess at where the electron is, the higher the value, the more likely it could be there when we measure it.)

Pretty cool, huh? The longer you wait, the less chance you have a guessing where it it correctly. The probability density melts as time marches on. Sometimes you can see little peaks of possible places it could be. The peaks at the end are a glitch in the video that I can't seem to fix. Those frames should be at the beginning. But remember, when you solve SE, you get the wave function, not the probability density function. So what does the quantum state look like? Well hold on, this looks pretty weird I think.

There are two lines. One of the "real" part of the wave function, the other is the "imaginary" part. Don't worry too much about this, this has to do with the imaginary number "i" that I mentioned before. The wave function is very strange. I think that's cool. So now you know what happens to an electron when you set it down. But what if you give it a push? The probability density:

And the wave function (just showing the real part this time):

 Let's talk about this for a second. First the probability density. It makes sense given what you just saw, right? You give the electron a kick to the right, it bounces off the wall and comes back. But what happens when you get near the wall? It gets a squiggly. Ever hear about atoms, light and other small objects acting like both waves and particles at the same time? This is where you can see it! When the electron gets near the wall, the waves that make it up interfere with each other, causing this weird squiggly effect you see when it gets near the wall! The wave function is a bit more obvious. It already looks like a wave. When parts of it bounce off the wall, they interfere with other parts. I think it looks pretty cool, what about you?

So that's it in a nutshell, there's more details that I might revisit at a later time, but they aren't that important right now. The videos were created with Python, using scipy, matplotlib, and mencoder. The source code is available if you're interested. As usual, comments and suggestions are encouraged!

Next up is the quantum mechanical version of the spring. I think this one is both really cool and important.

Schrödinger's Equation - Part 2

Okay, so last post we briefly introduced Schrödinger's equation. Mainly, we introduced the left hand side, which consists of the Hamiltonian, and the wave function. As a reminder, here is the equation once more.

On to the right hand side!

Schrödinger's Equation - Part 1

This is the start of where all the real quantum mechanics happens. Schrödinger's equation equation is what we use to calculate useful information about a quantum object or system of objects. Here it is...

 

Don't be afraid of it, it is difficult to solve, but not too difficult to understand. Through the next couple articles, I'm going to explain what it means, and why you should care.

A requirement and self evaluation

Just kidding. I have one more post that is off the intended track. For those that do not know, I've started this blog as a requirement for my science communication class here at the Colorado School of Mines.

If interested, read on.

Giving back

Greetings readers!

I have spent the last few posts discussing both introductory quantum mechanics material (the primary focus of this blog), as well as a more recent development in quantum theory and its applications. Quantum mechanics is a notoriously difficult topic. People like to use the words to make something out to be unexplainable or seem revolutionary. While quantum theory has been around for around a century, it is still a sort of buzz word. People hear quantum mechanics and tend to think it's magic, or that it's something only geniuses know.

Scientists as a whole have not done an excellent job in fixing this issue. The commonly implemented  "deficit" model of science communication is certainly prevalent in discussion of quantum mechanics. Sure, there are popular shows on the history channel, such as The Universe, and books such as The Elegant Universe that make certain aspects of quantum theory accessible to the layman. The question is, how many sources are there for the same material taught in a quantum physics class at a university? So far, I have found very little of it out there. The major sources lie on two extremes - the scientists unloading their research on the public, and the physics popularizers taking these ideas and condensing them into a simple idea. On one extreme, you have unintelligible papers filled with equation after equation. On the other, you feel like the information you've received has been so condensed that it is meaningless. Generally I find both of these extremes discuss the difficult concepts, and if you really want to understand the basics, you've got to head back to school and get a degree in physics.

I have found very little published in the middle, and my goal is to provide a source of basic quantum mechanics, and to apply these small steps towards bigger problems so that the next time you hear something about quantum mechanics in the news, in a book, in a movie, or on another blog, you can put it into context and grasp what it's actually saying.

While I have in mind what I would like to accomplish, I would like to take a step back and get feedback. I'm a physicist. I love physics, and applications or no, I find the subject absolutely fascinating. The problem is, this can blind me to what my readers are interested in. In science communication, information must be sent through multiple channels, and in multiple directions. If I am to accomplish my goals, I need engagement and feedback from my readers. I assume you have interest in quantum mechanics, at least on some level or you wouldn't be reading this. My question to you is, what additional content are you interested in? Find an interesting article? Send me a link! Confused about any of my posts? Let me know! Find an error in any of my posts? Rub it in my face!

One other thing. I try to keep up on other blogs, but if you find something similar to what I'm doing, I'd love to connect with other sources. If you're active on another blog, forum or other pipeline for science communication, link to my blog! I'd love to get more viewers and more feedback.

We will return in the next couple days with a post about the famous Schrodinger's equation. The first post will be an introduction, then I will delve into its uses and applications. I first have to go through some simple examples before we build up the know-how to tackle more interesting applications like atoms, molecules, and beyond.